|
研究材料徐变对结构的强度、刚度和稳定性影响的学科,是工程力学的一个分支。 徐变与松弛 徐变又称蠕变,是指材料在常应力作用下应变随时间缓慢增长的现象。许多材料,如混凝土、岩石、工程塑料和高温下的金属,都具有显著的徐变性质。常应力下的典型拉伸徐变曲线如图所示,OA为瞬时应变;AB为徐变的第一阶段,称为非定常徐变阶段;BC为徐变的第二阶段,称为定常徐变阶段;C点以后为第三阶段,又称为破坏阶段。材料所受应力和工作温度对徐变曲线的形状有很大的影响。
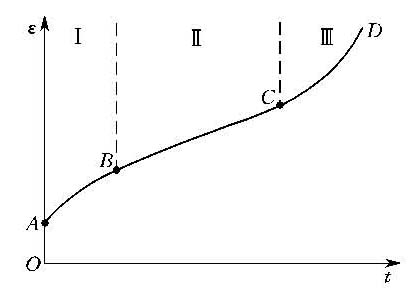
拉伸徐变曲线图
材料的徐变除影响结构的刚度外,还可能使结构的内力和应力发生变化。例如,当混凝土结构因强迫变形(变温、干缩或支座沉陷等)而引起应力状态时,徐变将使实际应力比弹性应力显著减少;在预应力钢筋混凝土构件中,徐变要引起构件预应力损失等。由于徐变而引起的应力随时间减少的现象称为松弛。 徐变物理方程 在徐变力学发展过程中,曾提出一些形式不同的物理关系,建立起徐变力学的各种计算理论,著名的有老化理论、流动理论、强化理论和继效理论等。这些理论的不同之处在于:老化理论假设徐变应变(εc)与应力(σ)、时间(t)具有某种函数关系,即εc=f(σ,t);流动理论假设徐变应变速率
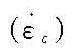
与应力、时间具有简单的函数关系,即
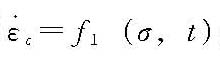
;强化理论假设徐变应变速率与应力、徐变应变有关,这种关系为
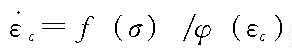
;继效理论则假设徐变是一种弹性或塑性后效,在线性条件下,继效理论中总应变的一般表达式为
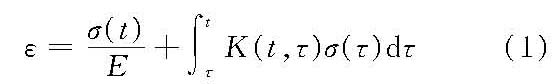
式中,右端第1项为瞬时应变;第2项为徐变应变;K为影响函数,表示时刻τ作用的应力对时刻t变形的影响;τ1为开始加载的龄期。 试验指出,老化理论和流动理论只适用于常应力作用下或应力变化很缓慢的情况,而强化理论和继效理论在变应力作用下也是适用的。上述徐变物理关系中,应力与应变的关系可以是线性的或非线性的。在平常温度和较低应力下,可采用简单的、近似的线性关系,在高温或高应力下,必须采用非线性的物理关系。各种关系可以推广到复杂应力状态,但都只在一定条件下近似反映材料的徐变性能。 徐变力学基本定理及其应用 水工混凝土结构的徐变分析通常采用线性继效理论。对于受刚性约束的匀质线性徐变体,在外来因素作用下,它的位移、应力与相应的瞬时弹性解答(指考虑该物体的弹性而不计其徐变性能时的解答)的关系归结为下面两个定理。 定理一:受刚性约束的线性徐变体,在外力作用下,其应力与相应的瞬时弹性应力相等,其位移与弹性位移的关系为
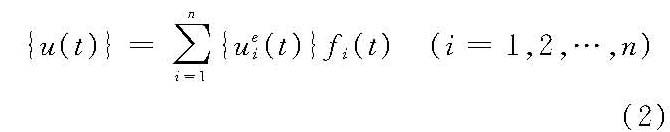
式中,{u(t)}为线性徐变体的位移;{uei(t)}为第i组比例荷载引起的瞬时弹性位移;fi(t)为与第i组比例荷载对应的、与荷载规律和徐变性质有关的时间函数。 定理二:受刚性约束的线性徐变体,由于强迫变形而引起的位移与瞬时弹性位移相等,其应力与弹性应力的关系为
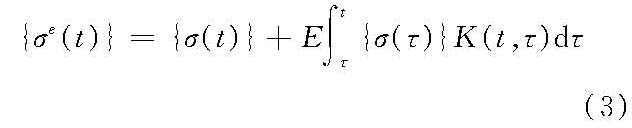
式中,{σe(t)}为瞬时弹性应力向量;{σ(t)}为线性徐变体的应力向量。 式(3)是以各应力分量σx、σy、…、τzx为未知量的独立的积分方程。 利用上面两个定理,可以求得受刚性约束的线性徐变体的应力和位移。对于受非刚性约束的线性徐变体,它的位移、应力与瞬时弹性解答没有简单的关系,可以采用数值法,将徐变当作初应变,用弹性力学中求解初应变问题的方法来解决徐变力学问题。 对高温下金属结构和机械零件进行徐变分析时,常用非线性流动理论。因为非线性徐变力学方程组的求解要遇到数学上的困难,所以工程设计中经常用近似解法,如变分法和参照应力法(reference stress method)等。后一方法是20世纪80年代以来得到迅速发展的一种有效方法。 对高应力下混凝土结构进行徐变分析时,可采用非线性继效理论。这时,可以在前述继效理论总应变的表达式中,分别用
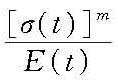
和
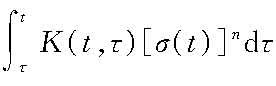
来表示应力与瞬时应变和徐变的非线性关系。在非线性徐变条件下,上述线性徐变理论的两个定理不再成立,需要用数值解法求得问题的解答。
|

