胡克定律

描述材料在弹性变形范围内内力与变形（或应力与应变）成正比的规律。胡克定律是弹性力学中的基本物理方程。由英国科学家胡克（R.Hooke）于1678年根据试验结果提出。

拉伸（压缩）胡克定律的表达式为

式中，σ为拉伸（压缩）试件的拉（压）应力；E为材料的纵向弹性模量；ε为纵向应变。纵向应变与横向应变的关系为

式中，ε′为横向应变；μ为横向变形系数，称为泊松比。

通过薄壁圆管纯扭转试验，可以建立剪切胡克定律

式中，τ为剪应力；γ为剪应变；G为剪切弹性模量。

对于各向同性的均质弹性体，以单向胡克定律为基础，应用叠加原理，可以导出三向应力状态下的胡克定律，称为广义胡克定律。

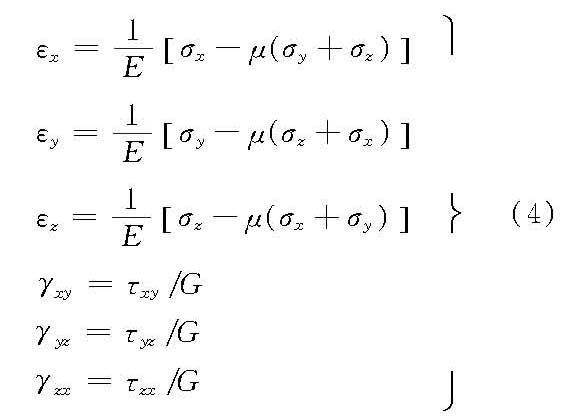
当一点的3个主应力已知时，可求得主应变。

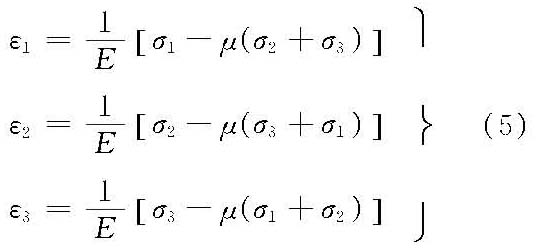
而γ₁2=γ₂3=γ₃1=0。显然，对于各向同性弹性体，只有两个独立的弹性常数，材料的性质与方向无关，主应力与主应变的方向相同。

可以将胡克定律写成下面的形式：

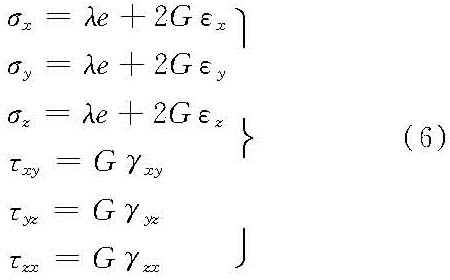
其中

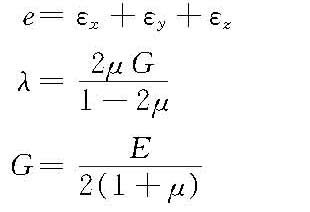
式中，e为体积应变；λ、G为拉密常数，Ｇ又称剪切弹性模量。

在平面应力情况下，σ_z=τ_yz=τ_zx=0，胡克定律简化为

如果将式（7）中的E变换为E/（1-μ²），μ变换为μ/（1-μ），并且σ_z=μ（σ_x+σ_y），便得到平面应变（ε_z=γ_yz=γ_zx=0）情况下的胡克定律。