|
为确定土石坝坝体、坝基及岸坡内的渗透要素和浸润线位置所进行的计算分析。渗透要素是指渗流区内的渗透流量、渗透流速、渗透坡降以及渗透压力等水力要素。浸润线是坝体内自由水面与坝体横剖面的交线。流经土石坝岸坡的渗流称为岸坡绕渗。 土石坝渗流具有自由水面,属于无压渗流。上下游水位不变时,渗透要素不随时间变化,土石坝渗流为恒定渗流,反之为非恒定渗流。如库水位降落时,土石坝坝体内形成的渗流随时间变化而变化。土石坝渗流分析主要是研究恒定渗流状态,特殊情况下,也需要研究其非恒定渗流状态。土石坝渗流属于空间问题,但通常作为平面问题处理。 土石坝渗流分析的目的为分析坝坡稳定,计算坝体应力和变形,判断坝体抗渗稳定性和为防渗排水设计提供依据。 土石坝渗流分析的方法有流体力学法、水力学法、流网法、数值计算法和模拟试验法。 流体力学法 土石坝渗流分析的解析法。此法的基本假定是:渗流是层流,服从达西定律。根据达西定律和渗流的连续方程所得的微分方程为
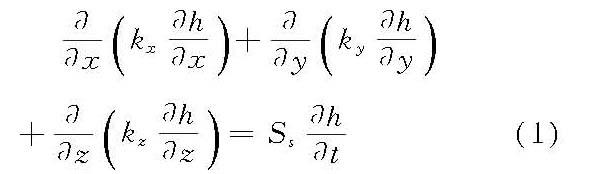
式中,h为渗流区的测压管水头;kx、ky、kz分别为沿x、y、z方向的渗透系数;Ss为单位水量,即单位体积的饱和土体在下降单位水头时,由于土体压缩所释放出来的水量。 在工程实践中,一般只考虑各向同性的平面恒定渗流(kx=ky),且不考虑土体的压缩性(Ss=0),则式(1)变为拉普拉斯方程
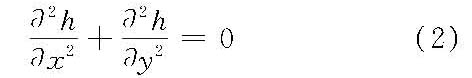
或
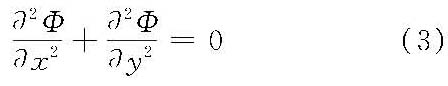
式中,Φ=-kh,称为流速势函数。流体力学法就是用解析法求出式(3)的解。 解拉普拉斯方程时,必须满足土石坝渗流区域的边界条件,如图1所示:①上游坝面的水下部分AO,h=H1;下游坝面的水下部分CD,h=H2。②坝基OD为不透水边界,
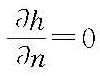
,n为不透水边界的法线方向。③下游坝坡渗流逸出段BC,h=y。④待求浸润线AB,需同时满足两个边界条件h=y和

0,n为浸润线的法线方向。结合具体的边界条件求解式(2)或式(3),就可求出流速势函数(Φ)和浸润线的位置,并由Φ求出任意点的渗透要素。也可根据所得的流速势函数求出其共轭流函数,并分别求出相互正交的等值线——等势线和流线,得到土石坝的流网,然后根据流网确定渗透要素。这种解析解只有在边界条件极为简单的少数情况下才能得到。在实际工程中,土石坝与坝基的边界条件复杂,求解析解极为困难,因而限制了流体力学法的应用。
水力学法 土石坝渗流分析的近似方法。土石坝渗流区域的大部分范围内,流线较平缓,属于缓变流,基本符合达西定律和杜平假定。 达西定律表达式为
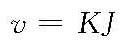
式中,v为渗流流速,cm/s;K为渗透系数,cm/s ;J为渗透坡降。 杜平假定为:坝体土料为均质,各向同性;渗流为缓变流,渗流场中任一铅直线上各点的流速和测压管水头是常数。
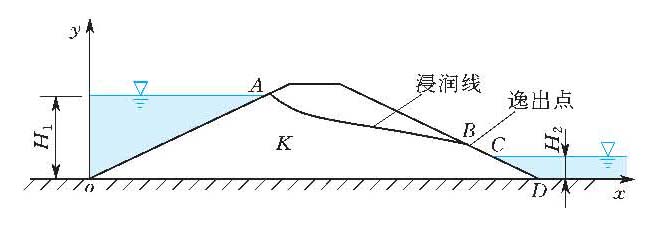
图1 土石坝渗流区域边界示意图
该方法只适用于平面渗流。由于对流线和渗流场的边界条件作了简化假定,只能得出某一渗流区域内的平均渗透要素及浸润线的位置。但其解答的精度,一般能满足实际工程要求,因此应用较为广泛,其原理和方法如下。 用铅直线代替其等势线,即认为铅直线上各点的流速和测压管水头都是常数。据此对底坡为零的缓变渗流(图2),可以用下列二式分别求出其单宽渗透流量(q)与浸润线。
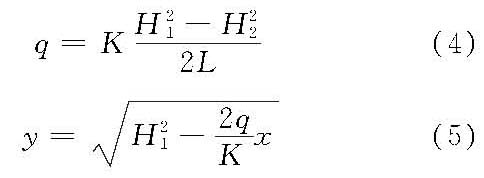
式中,x、y分别为浸润线上任意点的坐标;K为土料渗透系数;其余符号如图2所示。 水力学法解土石坝渗流问题时,常用铅直线(等势线)将土石坝横剖面划分成数段,利用各段渗流量相等的条件联立求解。 流网法 流网具有如下特性:等势线与流线相互正交;对于呈曲线正方形网格的流网,流网的每个网格的长宽比保持为常数,相邻等势线间的水头差Δh为常数,各相邻流线间的渗流量(-KΔh)也为常数。手绘流网法就是根据渗流区域的边界条件,首先确定边界流线和边界等势线,并初拟浸润线,然后按照流网特性用手勾绘并反复修改成正确的流网,以代替在流体力学法中用解析法解拉普拉斯方程所求得的流网,最后根据所绘流网求渗透要素。手绘流网法可以解决用计算方法不易解决的边界比较复杂的渗流问题,其精度可达到误差在5%以内。 数值计算法 有差分法和有限元法等。

图2 缓变渗流计算示意图
(1)差分法。用差分法求解拉普拉斯方程,一般用于稳定渗流。将渗流区域划分成有限个正方形网格,结合边界条件,以各网格交点处的测压管水头值(或流量值)为未知数,作一系列的差分方程式,然后联立求解各点的测压管水头值(或流量值)。在边界条件和筑坝土料复杂时,用差分法求解也较繁琐。 (2)有限元法。以变分原理求泛函极小值的方法求解符合定解条件(边界条件和初始条件)的渗流微分方程式,见式(1)。对于平面问题或空间问题,坝体渗流或绕坝渗流存在有渗流自由水面,由于自由面的位置和下游坝面逸出点位置是待求的,这类渗流分析是非线性问题,引用与非线性应力分析中类似于初应力的概念,提出有自由面渗流的初流量法和剩余流量法,通过对初流量值或剩余流量值的调整,可以将非线性分析转换成一系列的线性分析,迭代过程保持计算网格和总体传导矩阵不变。 先将求解域(Ω)剖分为n个单元,以各单元结点的水头值为未知数,将求泛函极值的问题化为求解线性代数方程组的问题。
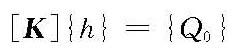
式中,[K]为总体传导矩阵;{h}为结点的水头,待求;{Q0}为等效结点流量,相当于弹性问题中的结点力。 由于自由面位置不确定,初始迭代所求得只是自由面近似位置,根据自由面上下区域之间没有流量交换的条件,通过反复迭代求得自由面和下游坝面逸出点的正确位置,由此得到渗流区域内各结点处的测压管水头值,据以计算渗流区域内的其他渗透要素。有限元法能解决土石坝复杂的边界条件、非均质的坝体和坝基及空间问题在内的土石坝渗流问题。 模拟试验法 模拟试验法有流体电拟法、缝隙槽法、土槽法以及电阻网络法和电阻电容网络法等。流体电拟法使用简便,应用很广。该法基于渗流运动与电流运动规律相似,用电势模拟测压管水头,用电流模拟水流。试验时,先拟定浸润线位置,在试验过程中予以修正。该法既可解决平面问题,也可解决空间的土石坝渗流问题。 各种渗流分析方法,需根据工程等级、地质条件、设计阶段以及渗流问题的复杂性等因素选用。一般可采用水力学法;对重要的大坝、高坝或必须按空间渗流考虑的问题,则采用有限元法、数值计算法或模拟试验法求解。
|

