连接上部结构与弹性地基的梁。基础梁的作用是将上部结构比较集中的荷载较均匀地分布到地基上，以减小地基压力的集度，保证结构和地基的稳定和安全。

基础梁的内力分析是一个重要而又复杂的问题。为了正确合理地分析地基与梁之间的相互作用，选择符合实际情况的地基模型和有效的计算方法是十分重要的。

地基模型

关于地基模型，已提出了多种假设。主要有文克勒地基、半无限大弹性地基和中厚度地基等。

（1）文克勒地基。1867年捷克文克勒（E.Winkler）假设地基单位面积上所受的压力与地基沉降成正比。这个假定实际上是用刚性底座上一系列互相独立的弹簧来模拟地基。按此假定，沉降只发生在地基的受压部分。实际上，沉降也发生在受压范围以外。

（2）半无限大弹性地基。1922年，苏联Г.Э.普罗克托尔假定地基为半无限大理想弹性体，采用弹性力学中半无限大弹性体的位移公式来计算地基的沉降量。现场试验表明，土是颗粒的集合体，几乎不能承受拉应力，过分加载后将产生流动而进入塑性状态。因此，必须在土中没有拉应力产生、塑性状态只限于极小区域时，才能看作弹性连续体。

（3）中厚度地基。假设地基为有限深弹性层，弹性层与刚性下卧层之间光滑接触或完全黏合，采用弹性层的位移公式计算地基沉降。此假设由中国徐芝纶和苏联扎马林（И.К.Замарин）于20世纪60年代初分别提出。

除上述假设外，有时还采用双参数地基、成层地基、折线地基、非弹性地基和各向异性地基假设等。

文克勒地基适用于计算极薄土层上的弹性基础梁，半无限大弹性地基适用于计算整岩地基或很厚土层上的基础梁，中厚度地基适用于计算中厚度土层上的基础梁。引用参数H/l（其中l为梁半长，H为土层厚度），当H/l≤0.25时，可按文克勒地基计算；当0.25≤H/l≤4.0时，宜按中厚度地基计算；当H/l≥4.0时，可按半无限大弹性地基计算。

基本方程

按照不同的计算假设，可以建立起相应的基础梁的求解方程。

（1）文克勒地基上基础梁的方程为

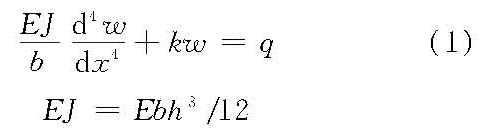
式中，w为梁的挠度；q为作用在梁上的荷载；E为梁的弹性模量；EJ为梁的弯曲刚度；h为梁的高度；b为梁的宽度；k为地基沉降系数（或称为基床系数）。

（2）半无限大弹性地基和中厚度地基上基础梁的方程是下列一组微分—积分方程。

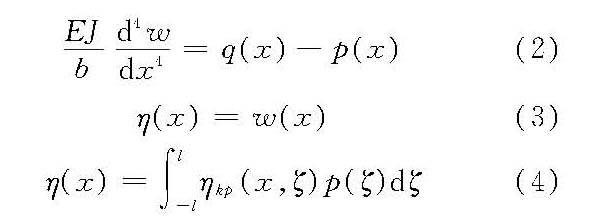
式中，η_kp为地基沉降函数；l为梁半长。

上述方程中，式（2）为梁的平衡方程；式（3）为梁与地基的连续方程；式（4）为地基沉降方程。

求解方法

有解析法和数值解法两类。

（1）解析法。主要有初参数法、幂级数法、复变函数保角变换法、积分变换法等。初参数法由苏联克雷洛夫（А.Н.Крылов）于1931年提出，是计算文克勒地基上梁的精确方法。幂级数法由苏联戈尔布诺夫—波萨多夫（М.И.ГорбуновПосадов）于1939年提出，主要用于半无限大平面或空间地基上的梁，是一种近似解法。复变函数保角变换法是求解折线边界（考虑地基开挖）上梁的一种有效解法。积分变换法是计算无限长梁或半无限长梁的主要方法。以上各种方法主要用于常截面的梁。

（2）数值解法。主要有连杆法、差分法、变分法、有限单元法等。连杆法由苏联热莫奇金（Б.М.Жемочкин）于1947年提出。该法把基础梁与地基之间的连续接触变换为连杆联系，然后用结构力学中的力法、位移法或混合法进行计算，原理简单，易于掌握，应用广泛，可适用于各种地基、变截面梁等。差分法可取地基反力和挠度作为未知数，也可仅以挠度作未知数，也是一种常用的方法。

在不易预先求得地基沉降量的情况下，例如非匀质地基、深度变化的中厚度地基以及其他复杂地基等问题，还在进一步研究之中。

基础梁除受梁上荷载作用外，有时还要考虑温度变化、边荷载等因素的影响。