|
采用以波陡(H/L)为小参量的幂级数展开的方法,考虑高阶非线性效应的有限振幅波。因由斯托克斯(G.G.Stokes)提出而得名。斯托克斯波也是一种无涡的、波面呈周期性振动的前进波。高阶的斯托克斯波的水质点运动轨迹虽仍接近于圆(深水)或椭圆(浅水),但是不闭合。水质点运动一个波周期后沿着波浪传播方向有一水平净位移,存在质量输移(mass transport)现象。一般,阶数愈高愈精确,但运算也愈繁难。 设流体为不可压缩、无黏滞性理想流体。运动为无涡的,其水流连续方程为拉普拉斯方程
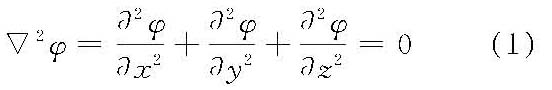
水底边界条件为
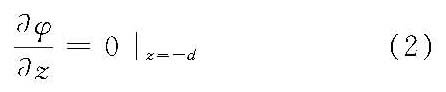
设将流速势函数φ和自由表面波面函数η两个未知量写成小参数ε的幂级数展开式
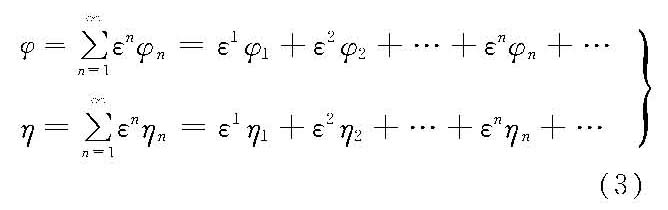
显然,每一项φn都是拉普拉斯连续方程式(1)的解,同时也满足水底边界条件和自由表面边界条件。在自由表面z=η(其水质点的初始位置为z=0),流速势函数(φ)用泰勒级数展开式可写成
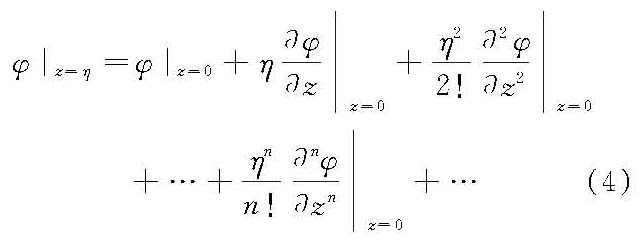
将式(4)引入非线性的自由表面z=η的运动条件:
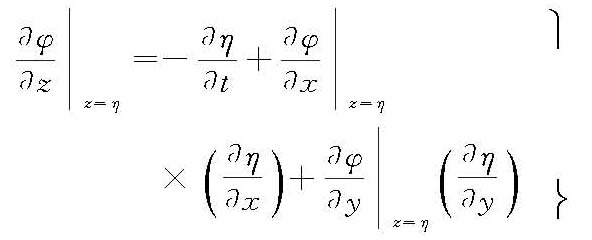
和自由表面z=η的动力条件:
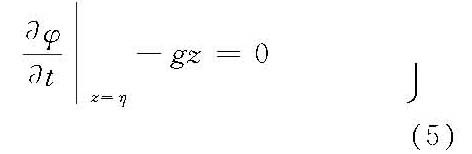
可得
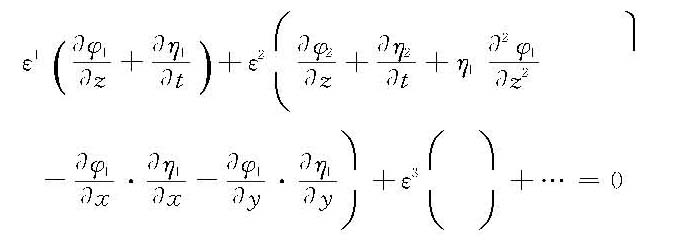
和
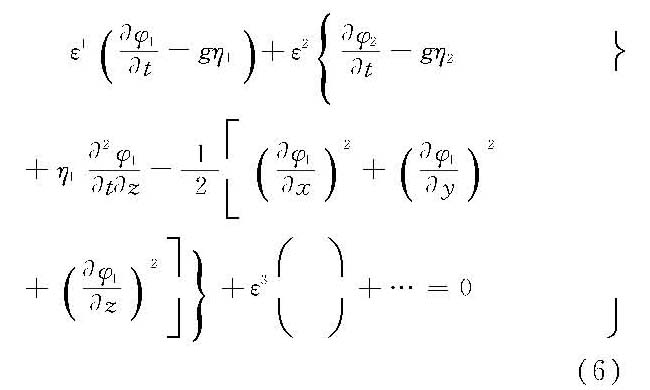
式(6)可分解成 一阶
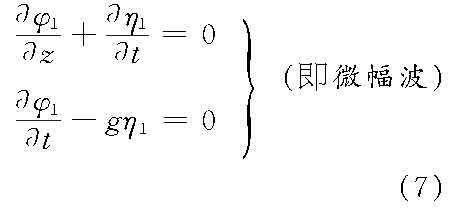
二阶
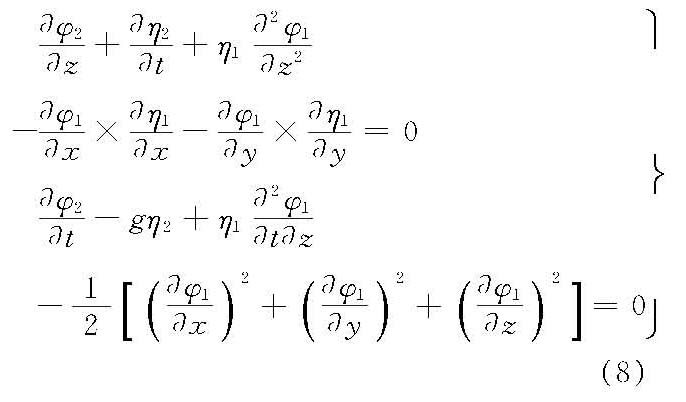
n阶
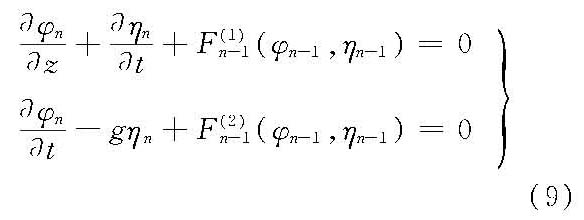
显然,一阶近似解就是线性微幅波。其余各阶可依次由已知的φn-1和ηn-1解出φn和ηn,都满足▽2φn=0和
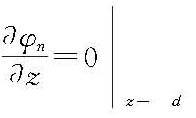
。
二阶斯托克斯波的基本特征值为: (1)流速势函数(φ2)
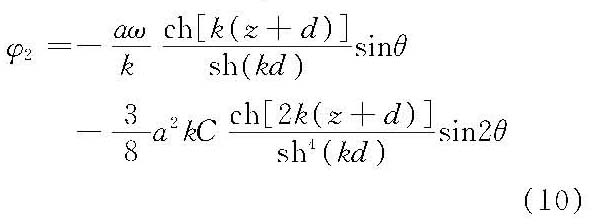
式中,ω为波圆频率,ω=2π/T;k为波数,k=2π/L;θ为相位角,θ=ωt-kx;a为波振幅;L为波长;T为波周期。 (2)波面函数(η2)
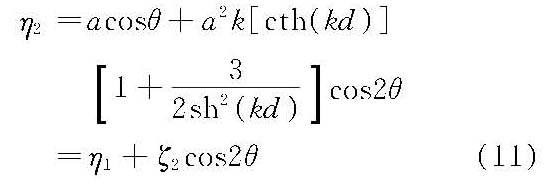
(3)波浪中线超高(ζ2)
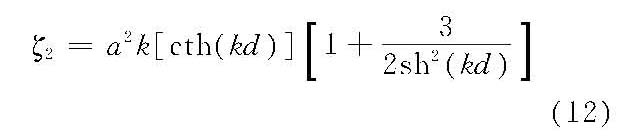
(4)波速(C2)
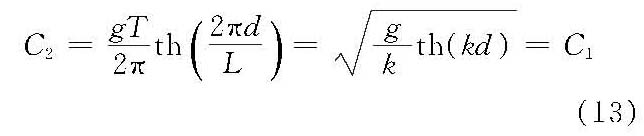
(5)质量输移速度
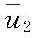
(一个波周期内的水质点的平均漂流速度)
无回流时
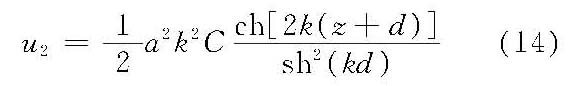
令d=L/2,代入式(10)~(14)即可得深水情况的二阶斯托克斯波结果。 二阶斯托克斯波的φ2和η2略去含a2k项,则得到一阶斯托克斯波即线性微幅波的流速势函数(φ)和波面函数(η)。 二阶斯托克斯波波面形状上下不对称,深水情况的自由表面处波浪中线超高ζ2=πH2/4L与格斯特纳(F.J.Gerstner)的有限振幅深水前进波一余摆线波的ζ相同。二阶斯托克斯波的波速(C2)与微幅波的波速(C)相等。当波陡较大、相对水深较小时,二阶斯托克斯波在波谷处将出现二级峰谷,这种情况宜采用高阶斯托克斯波。
|

