|
根据不规则波随机流体动力模型,按给定的目标谱(靶谱)模拟随机过程相应的数字序列。这可用于研究不规则波外观统计规律、不规则波与物体相互作用的概率和谱特性、波浪数学模型入射波随机过程的给定、不规则造波机随机信号源等。此方法比不规则波物理模型试验节省时间、费用低和便于推广,可与其相互补充,成为一种新的有效研究手段。不规则波数字模拟基本内容包括:①制定(或选择)随机模型;②确定模拟靶谱(理论或实测谱);③研制相应计算模式及编制软件;④利用计算机形成相应的随机数字时间序列(现实);⑤检验模拟过程现实的统计特性(如线性随机模型的正态性)和谱特性(靶谱与模拟谱的一致性);⑥研究模拟过程的外观统计特性;⑦研究不规则波与物体相互作用的概率和谱特性等。正确地选取不规则波随机数学模型及其模拟方法关系到数字模拟是否真实、可行。 不规则波的随机流体动力模型20世纪50年代以来,根据液体波动理论与概率论、随机过程理论相继提出了各种线性和非线性不规则波随机流体动力理论模型。按线性理论模型,不规则波是液体波动理论线性解析解的微幅波系随机叠加而成的三维随机过程,其表达简单,基本上反映天然波浪特性(平稳正态随机过程),便于统计分析,得到广泛应用。按非线性波理论模型,由于波系(谱分量)非线性相互作用,不规则波不具有正态概率特性,其表达式随非线性近似阶次增加而变得极其复杂,故表达式较为简化、线性频散关系(即频率只与波长及水深有关,而与振幅无关)仍适用的二阶近似非线性波模型获得较大进展。 不规则波线性理论模型皮尔逊模型 参见不规则波。 隆盖—希金斯模型 参见不规则波。 不规则波运动及动力要素线性模型 按液体波动线性理论解,不规则波的波面、压力、速度、加速度等运动及动力要素可概括表达为
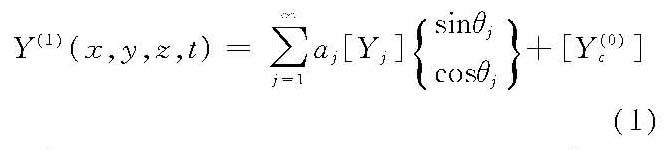
式中,θj=ξjx+ζjy-ωjt+εj,[Yj]为传递函数;[Y(0)c]为过程要素的均值,由线性波理论解给出。对于波动水面、点压力、水平速度及垂直加速度分量等取大括号中的cosθj,而对于波动速度势,垂直速度及水平加速度分量等则取sinθj。 上述三种线性模型皆可证明为渐近正态平稳过程。对于皮尔逊模型、隆盖—希金斯模型,其均值为零,相关函数为
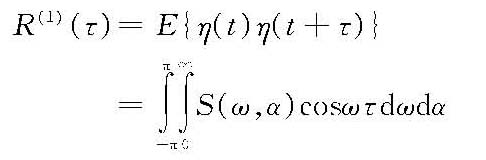
对于统一模式(1),其均值为[Y(0)c],相关函数为

其对应方差谱为
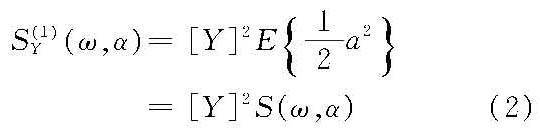
式中,E表示数学期望。 不规则波非线性模型基于波浪非线性相互作用二阶近似理论解,非线性不规则波运动及动力要素的统一随机模型可表为
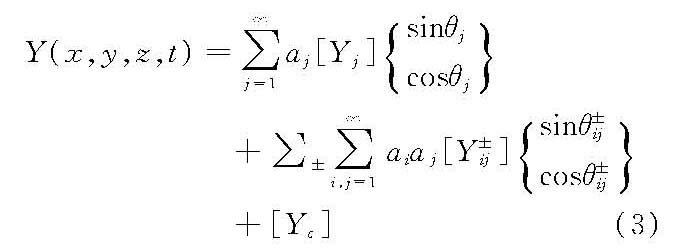
式右第1项为一阶近似项;第2项为非线性相互作用二阶非线性相互近似项;第3项为过程的要素均值;θ±ij=θi±θj;∑±表示分别取上标+、-号各项之和。式(3)为平稳非正态过程,其均值为[Yc],相关函数和谱分别为
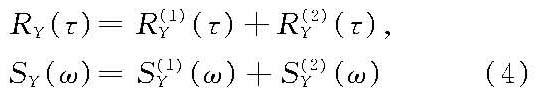
式中,R(2)Y(τ)和S(2)Y(ω)分别为二阶非线性相关函数和谱函数。 此外,还有将不规则波视为广义平稳随机过程,以广义傅立叶级数、傅立叶—斯蒂吉斯积分等来描述。 线性不规则波随机数字模拟 1960~1970年开始发表线性不规则波随机数字模拟研究成果,至今模拟理论与方法趋于完善,基本模拟方法可分为谱分量迭加法与线性滤波法。 谱分量叠加法为了模拟具有一维频率谱和二维方向频率谱的不规则波,须分别对频率分割离散为fn=nΔfn(n=1,2,…,N),αm=mΔαm(m=1,2,…,M),从而将不规则波表为N和N×M个谱分量随机迭代式。 谱分量离散方法 通常对方向频率谱的波向采用均匀分割离散αm=mΔα,Δα=const;对于频率分割采用:①等频率区间离散法fn=nΔf,Δf=fN/N,fN=Δt/2,Δt为采样周期,t=nΔt,TN=NΔt为模拟时间序列延时。②等能量法Sn=S(fn)Δfn=const,即将谱密度曲线在选定的模拟低频至高频区间内面积离散N个等分来确定Δfn的大小及位置,此时各谱分量的振幅相等,而频率区间则不等。等频率区间法则相反,各谱分量的振幅不相等。 随机模式 根据上述谱分量离散法,二维和三维随机波模式改写为
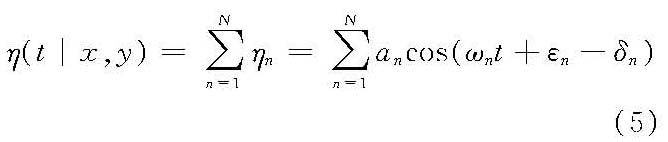
和
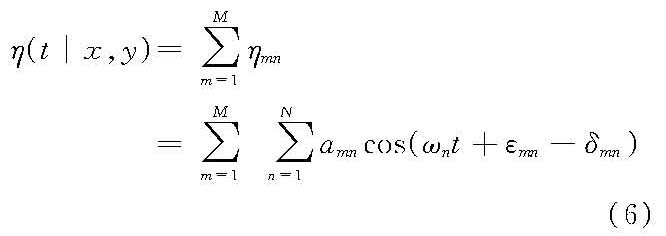
式中,δn=kn(xcosα0+ysinα0),α0为主波向;δmn=kn(xcosαm+ysinαm),αm为谱分量(ηmn)的波向;kn由线性频散公式(2πfn)2=gknth(knd)确定,d为水深;在0~2π之间均匀分布的随机相位(εn、εmn)可用蒙特卡罗法由计算机产生;谱分量振幅可按:①非确定性振幅法(NSA)a2mn=χ22S(fn,αm)ΔfnΔα,χ22系自由度ν=2的χ2ν分布,或②确定性振幅法(DSA)a2mn=2S(fn,αm)来给定。按NSA法模拟波是正态,模拟所产生的谱是随机的,而按DSA法模拟波只有谱分量足够大时为渐近正态,模拟所产生谱具有确定性。统计检验表明,当N>1024时此两种方法的模拟结果无显著差异。 计算模式 可采用:①直接求和法:适用于上述等能量离散情况,一般取M>30,N>200,直接计算三角函数求和;②快速傅立叶法(FFT),此法计算效率较高,适用于等频率离散情况,较常采用,其式由式(5)改写为
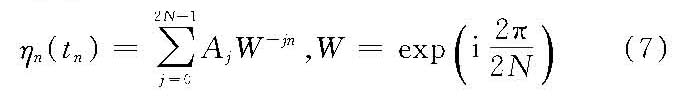
其中
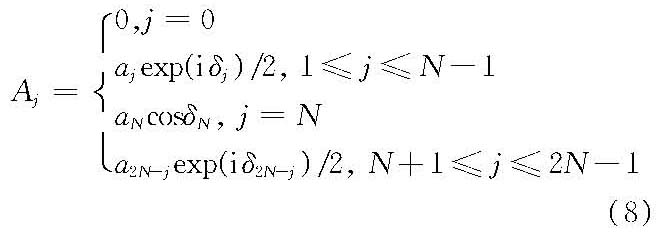
线性滤波法此法基本模式为下列的卷积式
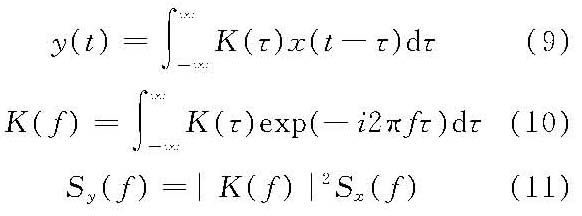
式中,y(t)、x(t)分别为系统的输出、输入;K(τ)、K(f)分别为系统响应函数、频率响应函数;Sy(f)为系统输出谱。 为了模拟具有单边频率谱Sη(f)的实随机波,可令
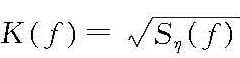
,x(t)为随机白噪声[即均值为零、方差谱为Sx(f)=1的正态随机过程],其离散计算模式为
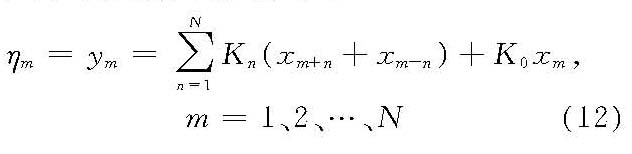
随机模拟归结为:由给定靶谱Sη(f)确定滤波权常数(Kn);由蒙特卡罗法产生均值为零、方差为1的正态随机时间序列(输入),按式(12)计算模拟波随机时间序列(输出)。线性滤波法所模拟的输出为具有给定靶谱的正态随机序列,且与N的大小无关,同时模拟波没有周期性重复,其缺点是按式(12)直接计算很费机时,也不便于模拟二维方向频率谱。 模拟现实的统计检验与分析为了验证所采用的模拟模式与计算方法的正确性与适用性,须对所产生的随机时间序列进行统计检验,主要包括模拟现实谱与靶谱的一致性,随机现实的平稳性与正态性,进而可对之进行随机波外观统计特性如波要素、极值、波群等统计分析。 非线性不规则波的随机数字模拟由于制定非线性波高阶近似随机流体动力模型及其实施方法难度极大,1979年开始探讨二阶非线性波的模拟及其应用,其中主要问题为非线性靶谱分离线性分量,传递函数的计算及改换为便于快速计算的FFT模式等。高阶非线性波模拟有待研究突破。
|

