欧拉方程

微分形式的理想流体动量方程或运动方程。在理想流体中，忽略黏滞性作用，所以切应力等于零，作用在流体上的力只是质量力和压力。根据牛顿第二定律建立流体微团所受的力和其加速度之间的关系式，如图所示，得到欧拉方程在直角坐标系中的形式为

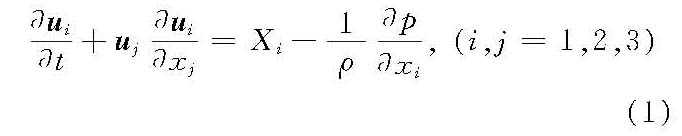
式中，对于一项中两次出现的脚标‘j’表示从1到3求和，i=1，2，3分别对应x_i坐标轴方向；X_i为x_i坐标轴方向的单位质量力；p为压强；u_i为在x_i坐标轴的分速度。这是瑞士数学家、力学家L.欧拉于1755年首先提出的。欧拉方程表达了流体的压强、单位质量力和加速度之间的关系。它与连续方程组成微分方程组，为求解压强和流速场建立了必要而充分的条件。

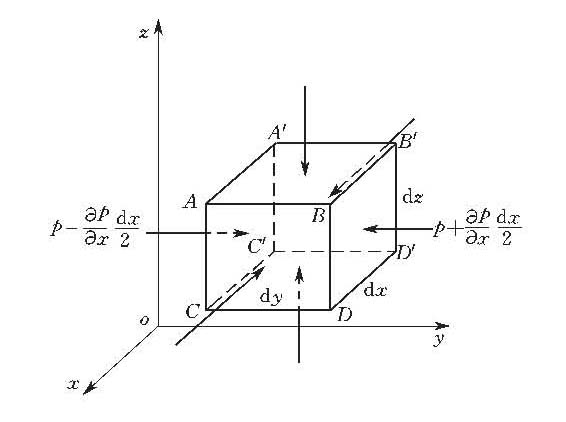
微六面体示意图

当流体处于恒定流状态，作用于流体的质量力只是重力的情况下，沿流线对欧拉方程进行积分，可以得到水力学中普遍应用的伯努利方程。当流体处于平衡状态时，欧拉方程的形式为

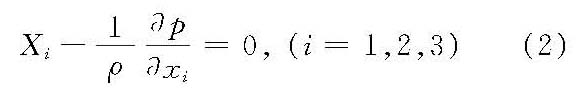
其物理意义是：在平衡状态下，流体静压强沿某一方向的变化率与该方向的单位质量力相等。欧拉方程的建立，为研究静止的和流动的理想流体问题奠定了重要的理论基础。